Quantum Energy Calculation with VQE ⚡
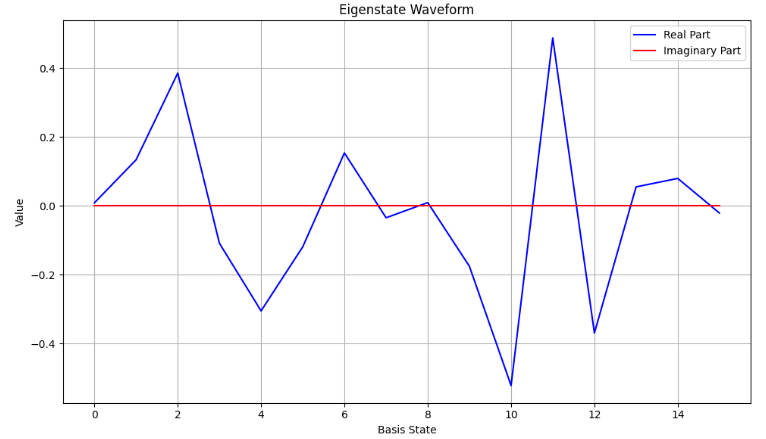
Waveform
Introduction
This project demonstrates the application of Variational Quantum Eigensolver (VQE) in solving quantum energy calculation problems. VQE is a quantum algorithm used to find the lowest energy state (eigenvalue) of a given Hamiltonian, which has broad applications in fields such as quantum chemistry and material science.
Features 🖥
- Quantum Energy Calculation: Utilize VQE algorithm to compute the lowest energy state of a given Hamiltonian.
- Hamiltonian Definition: Define the Hamiltonian terms corresponding to the system under study.
- Ansatz Circuit: Configure the ansatz circuit using
TwoLocalfor quantum state preparation. - Optimizer Setup: Implement the SPSA optimizer to minimize the energy and find the ground state.
- Quantum Visualization: Visualize the eigenstate using Bloch sphere representation.
Installation 🛠
-
Clone the repository:
git clone https://github.com/mkswagger/teamheisenberg_quantathon/
-
Install required dependencies
pip install -r requirements.txt
Usage ✍🏼
- Open the main.py file and adjust the Hamiltonian terms for your specific system.
- Run the script:
python main.py
- View the computed eigenstate, eigenvalue, and Bloch sphere visualization.
VQE Workflow 📚
The VQE algorithm consists of the following steps:
-
Quantum Circuit Preparation (Ansatz): Construct an ansatz circuit that prepares a quantum state parametrized by variational parameters. This circuit will be optimized to minimize the energy expectation value.
-
Measurement and Energy Calculation: Execute the ansatz circuit on a quantum computer and perform measurements to estimate the energy expectation value of the Hamiltonian.
-
Optimization: Use classical optimization techniques to adjust the variational parameters iteratively, minimizing the energy expectation value. This process converges towards the lowest energy state.
Application to Hydrogen Atom
The hydrogen atom serves as a model system for our demonstration. Its Hamiltonian includes terms for the electron’s kinetic energy, the electron-nucleus attraction potential, and the electron’s self-potential. By mapping this Hamiltonian onto a quantum circuit and leveraging VQE, we can approximate the ground state energy and its corresponding quantum state.
Bloch Sphere Visualization
The Bloch sphere is a geometrical representation of a qubit’s quantum state. After executing the VQE circuit, the obtained eigenstate can be depicted on the Bloch sphere. The direction of the Bloch vector signifies the orientation of the quantum state, while its length represents the probability distribution. This visualization aids in intuitively understanding the obtained eigenstate.
Real-World Application: Quantum Chemistry
Quantum chemistry involves studying molecular systems using quantum mechanics. VQE’s ability to approximate ground state energies is crucial for simulating molecular structures, reactions, and electronic properties. By applying VQE to molecular Hamiltonians, we gain insights into chemical reactions and materials’ behavior that are challenging to compute classically.
Comparison and Impact
Comparing VQE’s energy estimates with classical methods provides a benchmark for accuracy and efficiency. VQE’s quantum parallelism accelerates certain calculations, enabling the exploration of larger molecules and complex systems. Although VQE’s results may be affected by noise in current quantum hardware, it showcases quantum computing’s potential in solving intricate problems.
Conclusion ✨🔍
VQE presents a powerful approach to tackle Hamiltonian equations and determine the lowest energy states of quantum systems. By applying VQE to the hydrogen atom and real-world quantum chemistry problems, we unlock new possibilities for molecular simulations and material science. The Bloch sphere visualization and comparison with classical methods underscore VQE’s impact in quantum computations.
Future Enhancements 🔬
To further improve VQE, consider the following enhancements:
- Incorporate noise models to simulate real-world quantum devices.
- Explore advanced ansatz circuits for improved accuracy.
- Integrate parameter optimization techniques for better convergence.
Acknowledgments 🦾
Special thanks to the Quantum Computing community for their valuable resources and insights.